Cluster Analysis using R

In this post, I will explain you about Cluster Analysis, The process of grouping objects/individuals together in such a way that objects/individuals in one group are more similar than objects/individuals in other groups.
 For example, from a ticket booking engine database identifying clients with similar booking activities and group them together (called Clusters). Later these identified clusters can be targeted for business improvement by issuing special offers, etc.
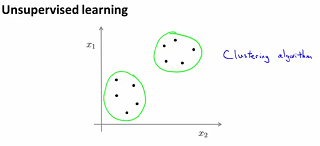
Cluster Analysis falls into Unsupervised Learning algorithms, where in Data to be analyzed will be provided to a Cluster analysis algorithm to identify hidden patterns within as shown in the figure below.

 In the image above, the cluster algorithm has grouped the input data into two groups. There are 3 Popular Clustering algorithms, Hierarchical Cluster Analysis, K-Means Cluster Analysis, Two-step Cluster Analysis, of which today I will be dealing with K-Means Clustering.
Explaining k-Means Cluster Algorithm: 
In K-means algorithm, k stands for the number of clusters (groups) to be formed, hence this algorithm can be used to group known number of groups within the Analyzed data.
K Means is an iterative algorithm and it has two steps. First is a Cluster Assignment Step, and second is a Move Centroid Step.
CLUSTER ASSIGNMENT STEP: In this step, we randomly chose two cluster points (red dot & green dot) and we assign each data point to one of the two cluster points whichever is closer to it. (Top part of the below image)
MOVE CENTROID STEP: In this step, we take the average of the points of all the examples in each group and move the Centroid to the new position i.e. mean position calculated. (Bottom part of the below image)
The above steps are repeated until all the data points are grouped into 2 groups and the mean of the data points at the end of Move Centroid Step doesn’t change.

 By repeating the above steps the final output grouping of the input data will be obtained.

Cluster Analysis on Accidental Deaths by Natural Causes in India using R 

Implementation of k-Means Cluster algorithm can readily downloaded as R Package, CLUSTER . Using the package we shall do cluster analysis of Accidents deaths in India by Natural Causes.

Steps implemented will be discussed as below: 

The data for our analysis was downloaded from www.data.gov.in.

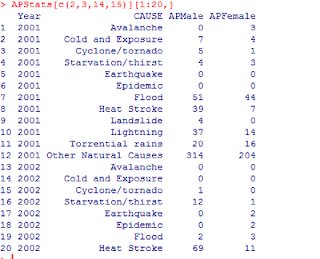
Between 2001 & 2012. Input data is displayed as below: 

For any cluster analysis, all the features have to be converted into numerical & the larger values in the Year Columns are converted to z-score for better results. 

Run Elbow method (code available below) is run to find the optimal number of clusters present within the data points. 

Run the K-means cluster method of the R package & visualize the results as below:

Code:

#Fetch data

data= read.csv("Cluster Analysis.csv")

APStats = data[which(data$STATE == 'ANDHRA PRADESH'),]

APMale = rowSums(APStats[,4:8])

APFemale = rowSums(APStats[,9:13])

APStats[,'APMale'] = APMale

APStats[,'APFemale'] = APFemale

data = APStats[c(2,3,14,15)]

library(cluster)

library(graphics)

library(ggplot2)

#factor the categorical fields

cause = as.numeric(factor(data$CAUSE))

data$CAUSE = cause

#Z-score for Year column

z = {}

m = mean(data$Year)

sd = sd(data$Year)

year = data$Year

for(i in 1:length(data$Year)){

z[i] = (year[i] - m)/sd

}

data$Year = as.numeric(z)

#Calculating K-means - Cluster assignment & cluster group steps

cost_df <- data.frame()

for(i in 1:100){

kmeans<- kmeans(x=data, centers=i, iter.max=100)

cost_df<- rbind(cost_df, cbind(i, kmeans$tot.withinss))

}

names(cost_df) <- c("cluster", "cost")

#Elbow method to identify the idle number of Cluster

#Cost plot

ggplot(data=cost_df, aes(x=cluster, y=cost, group=1)) +

theme_bw(base_family="Garamond") +

geom_line(colour = "darkgreen") +

theme(text = element_text(size=20)) +

ggtitle("Reduction In Cost For Values of 'k'\n") +

xlab("\nClusters") +

ylab("Within-Cluster Sum of Squares\n")

clust = kmeans(data,5)

clusplot(data, clust$cluster, color=TRUE, shade=TRUE,labels=13, lines=0)

data[,'cluster'] = clust$cluster

head(data[which(data$cluster == 5),])